ARTICLES

1. The “Bipartite Reading” and the internal unity of language and logic

The Tractatus’ account of propositions in terms of pictures, as is well recognised, directly applies only to what Wittgenstein calls elementary propositions; an elementary proposition – the “simplest kind of proposition” (TLP 4.21)¹ – is a “nexus, a concatenation of names” (TLP 4.22), and it has a pictorial nature because its elements (names) are combined in the same way as the elements of its corresponding state of affairs. Wittgenstein’s account of molecular – complex – propositions (among which, importantly, propositions of logic are to be found) on the other hand, relies on the idea that they are truth-functions of elementary propositions, namely propositions whose truth-value is determined by the truth-value of their constituent propositions; examples of such propositions are those obtained by the application of familiar truth-functional connectives such as ‘~’ (negation), ‘&’ (conjunction), ‘v’ (disjunction), and so forth. As section 5 of the Tractatus reads: “A proposition is a truth-function of elementary propositions”. One the one hand, therefore, we have elementary propositions, which directly picture states of affairs, and on the other we have molecular propositions – truth-functions of elementary propo-sitions.

This brief summary of the Tractatus’ conception of the nature of the proposition encourages the thought that the Tractatus’ account of language and logic rests on two different principles: the principle of pictorial representation (which accounts for elementary propositions), and the principle of truth-functionality (accounting for molecular and quantified propositions, and also, therefore, for logical complexity); on this view, then, it seems as if – as Elizabeth Anscombe has it – “[t]he whole theory of propositions is […] a merely external combination of two theories: a ‘picture theory’ of elementary propositions (viz. that they have meaning by being ‘logical pictures’ of elementary states of affairs), and the theory of truth-functions as an account of non-elementary propositions” (1959: 25-26). This is the view actually endorsed by Georg von Wright, according to whom “Wittgenstein’s Tractatus may be called a synthesis of the theory of truth-functions and the idea that language is a picture of reality” (1955: 533); K. T. Fann, similarly, holds that “Wittgenstein’s theory of language in the Tractatus has two components: the ‘picture theory’ and the ‘truth-function theory’” (1969: 8).

This reading of Wittgenstein’s analysis of language and logic in the Tractatus I call the “bipartite reading”; although perhaps a natural way of conceiving of the relation between elementary and molecular propositions in the Tractatus, the bipartite reading seems also problematic in many respects. Brian McGuinness expresses his worries about it in the following terms:

[I]n the first part of the Tractatus […] we seem to be told that the essence of a proposition is to be a picture, while in the later parts we are told that its essence is to be a truth-function […]. [A] […] serious difficulty is that the two accounts seem to be quite separate things, and, if this is so, cannot both be adequate accounts of what it is to be a proposition. (2002: 65-66)

More recently, Michael Morris argued:

There is a risk of understanding Wittgenstein’s account of language […] as falling into two completely unconnected parts: one which is appropriate to the conception of elementary sentences as models, the other which concerns the construction of other sentences out of elementary sentences. (2008: 234)

The bipartite reading, therefore, by holding that Wittgenstein has an account of the nature of elementary propositions and a different (unrelated) one of molecular propositions, seems to make the relation between elementary and molecular propositions mysterious (i.e. it does not explain it at all); furthermore, the bipartite reading is hard to reconcile with Wittgenstein’s idea that there is a general propositional form, that is, a common essence to all propositions (elementary and molecular, empirical and logical ones, and so forth), which is, on the other hand, something the Tractatus is clearly committed to (cf. TLP 4.5).

The fact that there is some stringent (internal) relation between truth-functional articulation (and thus also logical complexity) and a proposition’s ability to express its sense is something that Wittgenstein acknowledged very early. In 1912, when he was still studying under Russell, and when the two were mainly discussing the nature of logic and the status of logical propositions, Wittgenstein wrote to Russell:

I believe that our problems can be traced down to the atomic propositions. This you will see if you try to explain precisely in what way the Copula in such a proposition has meaning.

     I cannot explain it and I think that as soon as an exact answer to this question is given the problem of ‘v’ and of the apparent variable will be brought very near to their solution if not solved. (NB: 121)

A solution to the problem of explaining the nature of logical complexity (what Wittgenstein refers to as the problem of ‘v’) will be achieved by a correct explanation of the role of the copula in a atomic proposition; the suggestion thus amounts to the idea that an account of logical complexity will be given by an explanation of propositional articulation at the elementary level.

In Wittgenstein’s wartime Notebooks we find a similar view of the relation between the nature of propositions and of logical articulation. As regards the latter, Wittgenstein writes: “The problems of negation, of disjunction, of true and false, are only reflections of the one great problem in the variously placed great and small mirrors of philosophy” (NB: 40), where the one great problem is identified by Wittgenstein as that of giving an explanation of the nature of the proposition: “My whole task consists in explaining the nature of the proposition” (NB: 39). This passage suggests that the problems related to logical complexity (“the problems of negation, of disjunction” etc.) will be solved by an account of the nature of the proposition. This attests that Wittgenstein felt there cannot be any dualism between an account of the nature of the proposition and an account of logical complexity. These are simply two aspects of the same problem, which are to be given the same solution.

To observe that the bipartite reading is a problematic interpretation of the Tractarian conception of the relation between elementary and complex propositions is by no means a particularly novel (or very controversial) proposal. Peter Winch has long ago argued:

[I]t is vital to our understanding of Wittgenstein to see that the nature of logic is already being inquired into in Wittgenstein’s treatment of the puzzle about the relation between propositions and facts. This point can perhaps be expressed in the form of another problem: what is the relation between a proposition’s ability to state a fact and its ability to stand in logical relations to other propositions? Now Wittgenstein thought […] that there must be such a relation; that it is not merely a contingent matter that a proposition can combine these two functions; that unless propositions had logical relations with each other they would not state facts (i.e. would not be propositions) and unless they stated facts, they would not have logical relations with other propositions. (1969: 3-4)

In the same vein, Marie McGinn writes:

Wittgenstein is convinced that we shall see everything clearly – the nature and the status of the propositions of logic, negation, disjunction, inference, truth and falsity – when we see this one thing clearly: the nature of a proposition. […] [C]oming to see the nature of the proposition clearly is, at the very same time, coming to see negation and the status of the propositions of logic clearly: we have here, not a number of separate problems, but one great problem. If the problem is to be solved, then it must be solved all at once and in its entirety. The idea of the single great problem is that once the nature of a proposition has become clear, then everything will be clear: the nature and status of the propositions of logic, the nature of negation, inference, and so on. (2006: 15-16)²

But how does Wittgenstein, in the Tractatus, implement and develop the idea that the nature of logical complexity is grounded in, and even exhausted by, an account of the nature of the (elementary) proposition? In short, Wittgenstein holds that all logical constants are already present in an elementary proposition, that is, in a proposition which, by being an immediate combination of names, is a picture of reality. We have statements of this position in the Notebooks:

[I]f the positive fact φa is given then so is the possibility of (x).φx, ∼(∃x) φx, ∼φa etc. etc. (All logical constants are already contained in the elementary proposition). (NB: 27)³

And in the Tractatus we find:

An elementary proposition really contains all logical operations in itself. For ‘fa’ says the same thing as

‘(∃x) . fx . x = a ’.

Wherever there is compositeness, argument and function are present, and where these are present, we already have all the logical constants. (TLP 5.47)

The basic idea of these passages seems clear (logical complexity is already given as soon as elementary compositeness is given); however, we are still in need of a full account of the view that the nature of logic is to be clarified by a correct account of the nature of elementary propositions. Although, as seen, many interpreters are aware of the shortcomings of the bipartite reading, one looks rather in vain in the secondary literature for a full and detailed account of the Tractatus’ view that all logical constants are already present in an elementary proposition, and thus for an account of the Tractatus’ conception of the unity of language and logic; this idea has never been, it seems to me, fully discussed⁴ or very persuasively explained. Our task in the rest of this paper is to provide such an explanation.

2. Logical constants, operations and functions

At 5.2341 Wittgenstein writes: “Negation, logical addition, logical multiplication, etc. etc. are operations”. Thus Wittgenstein’s claim at 5.47 that an elementary proposition contains all logical constants means that it contains all logical operations; in order to understand Wittgenstein’s account of the unity of language and logic, which depends on the claim that all logical operations are present in an elementary proposition, we must clarify his notion of an operation.

Wittgenstein presents and discusses this notion as follows:

The structures of propositions stand in internal relations to one another. (TLP 5.2)

In order to give prominence to these internal relations we can adopt the following mode of expression: we can represent a proposition as the result of an operation that produces it out of other propositions (which are the bases of the operation). (TLP 5.21)

An operation is the expression of a relation between the structures of its result and of its bases. (TLP 5.22)

The operation is what has to be done to one proposition in order to make the other out of it. (TLP 5.23)

Finally, the notion of an operation is connected to that of a truth-function, which at 5 was employed in order to define the notion of a (molecular) proposition. “Truth-functions of elementary propositions are results of operations with elementary propositions as bases. (These operations I call truth-operations.)” (TLP 5.234). As said, Wittgenstein applies this truth-functional account to all propositions. “All propositions are results of truth-operations on elementary propositions” (TLP 5.3).

In the Tractatus Wittgenstein famously rejects the assimilation of operations to functions: “Operations and functions must not be confused with each other” (TLP 5.25). As Peter Hylton – following Max Black – says, however, it appears as if “everything, or almost everything, that Wittgenstein says about operations could with equal correctness be said about functions” (2005: 140, and see Black 1964: 258-260). For example, the claim that no statement is made by an operation (TLP 5.25) seems hardly helpful in distinguishing operations and functions, for no statement is made by a function either; the function x ², for instance, does not assert anything. Likewise, the fact that “[a] function cannot be its own argument, whereas an operation can take one of its own results as its base” (TLP 5.251) does not seem to distinguish functions from operations, for surely operations themselves cannot be operated on; what can be operated on is the result of an operation (a proposition, a truth-function in Wittgenstein’s terminology), but, likewise, the result of the saturation of a function with an argument (its value) can, at least in some cases, be an argument of that very function.

According to Hylton (2005: 141 ff.), when Wittgenstein opposes operations and functions he has in mind Russell’s and Whitehead’s notion of a propositional function, as that notion is discussed in Principia Mathematica;⁵ and, in fact, Russell and Whitehead discuss sentential connectives precisely in terms of propositional functions (“aggregations of propositions” in their terminology). “An aggregation of propositions […] into a single proposition more complex than its constituents, is a function with propositions as arguments” (1910: 6). The resulting proposition (the value of the function) is a complex or molecular proposition. Russell and Whitehead (1910: 6-7) identify four important cases of aggregations of propositions: the “Contradictory Function”, the “Logical Sum” (also called “Disjunctive Function”), the “Logical Product” (or “Conjunctive Function”) and the “Implicative Function”, which correspond to the sentential connectives of “negation”, “disjunction”, “conjunction”, and the “material conditional”. Thus, what Wittgenstein conceives of as operations, Russell and Whitehead conceive of in terms of propositional functions.

At 5.251, let us recall, Wittgenstein remarks that “[a] function cannot be its own argument, whereas an operation can take one of its own results as its base”. While an operation, “negation” for instance, can be applied to the result of its own application, the “propositional function”, say, “x is wise”, cannot take one of its values as argument: that is, the proposition “Socrates is wise” (one of the values of the propositional function “x is wise”) cannot itself be an argument of that very propositional function: “Socrates is wise is wise” is nonsense (see Russell and Whitehead 1910: 43). A further reason for Wittgenstein’s distinction between functions and operations, as seen, is that “no statement is made by an operation, but only by its result, and this depends on the bases of the operation” (TLP 5.25). As Hylton (2005: 145) notices, however, Russell and Whitehead (1910: 18, 96-97) discuss (and admit) precisely the notion of asserting a propositional function, that is, of asserting any value of the propositional function in question, where a propositional function is defined as “a statement containing a variable x, and such that it becomes a proposition when x is given any fixed determined meaning” (Russell and Whitehead 1910: 15).⁶

If Wittgenstein contrasted his notion of an operation with that of a propositional function, the possibility seems open of assuming that he might have held that operations are (mathematical) functions, in roughly the way Frege thought.⁷ The proposal of identifying an operation with the mathematical notion of a function (as opposed to that of a propositional function) however, makes little sense. In general, a function takes an object (or more than one) as argument and delivers an object as value; that is, it maps objects onto objects. But an operation delivers a proposition as a result, and a function that delivers a proposition as value just is a propositional function. There are, however, deeper reasons for resisting the identification of operations and functions. On a Fregean view, the functional conception of propositional complexity can be extended, with the introduction of some particular functions (truth-functions), to account for logical relations between propositions; thus, on a Fregean account, the relation that a propositional constituent (a name for instance) has to the proposition of which it is a constituent is in principle no different from the relation a proposition has to the more complex proposition of which it is a constituent. A proposition, on this account, occurs in another in no different way from how a sub-propositional constituent occurs in a proposition; both are arguments of some functions (see Sullivan 2000: 178). In the Notes Dictated to Moore, however, Wittgenstein remarks, contra Frege:

There are internal relations between one proposition and another; but a proposition cannot have to another the internal relation which a name has to the proposition of which it is a constituent, and which ought to be meant by stating it ‘occurs’ in it. In this sense one proposition can’t ‘occur’ in another. (NM: 116)⁸

There is a clear rejection, here, of the assimilation of logical operations to functions.

As we saw, the Tractatus characterises an operation as “what has to be done to one proposition in order to make the other out of it” (TLP 5.23). This suggests that an operation, is “less like an entity, that might be a constituent of a more complex entity, than it is something that we do” (Hylton 2005: 152), that is to say, some kind of procedure or process. In fact, Wittgenstein discusses operations in terms of rules for constructing propositions. At 5.512 he writes:

[I]n ‘~p’ it is not ‘~’ that negates; it is rather what is common to all the signs of this notation that negate p.

That is to say the common rule that governs the construction of ‘~p’, ‘~~~p’, ‘~p v ~p’, ‘~p .~p’, etc. etc. (ad inf.). And this common factor mirrors negation.

The expression of an operation should not be confused with the operation itself. In ‘~p’, it is not the symbol ‘~’ that negates, as well as in ‘p . q’, it is not the ‘.’ that conjuncts. The negative factor in ‘~p’ is represented, says Wittgenstein, by ‘what is common to all the signs of this notation that negate p’. That common element (the operation ‘negation’) is a rule that governs the construction of propositions in which ‘p’ is negated. In ‘p . q’, on the other hand, the conjunctive element (the operation ‘conjunction’) is what is common to all propositions that affirm both ‘p’ and ‘q’, and what is common to these propositions is having been constructed according to the same rule.

Importantly, the existence of operations, of rules for constructing propositions, seems for Wittgenstein to depend on the establishment of a language. As soon as we have a language, we have rules for truth-operations; this is, I believe, what Wittgenstein means when he says that operations are in place once a notation has been established:

Once a notation has been established, there will be in it a rule governing the construction of all propositions that negate p, a rule governing the construction of all propositions that affirm p, and a rule governing the construction of all propositions that affirm p or q: and so on […]. (TLP 5.514)

Operations are thus not something over and above the workings of propositions of language, but are rules for constructing propositions (the results of operations) given other propositions (the bases of the operations). In the next two sections we will consider in detail Wittgenstein’s conception of an operation from the Notes on Logic to the Tractatus, and we will see in what sense operations are in place when a language is established. This will finally put us in a position to see fully why – as Wittgenstein claims at 5.47 – an elementary proposition really contains all logical operations in itself, and thus why the bipartite reading cannot be a correct interpretation of Wittgenstein’s views on language and logic.

3. Language and logic in the Notes on Logic

In the 1913 Notes on Logic Wittgenstein conceives of propositional sense in terms of bipolarity:

Every proposition is essentially true-false: to understand it, we must know both what must be the case if it is true, and what must be the case if it is false. Thus a proposition has two poles, corresponding to the case of its truth and the case of its falsehood. We call this the sense of a proposition. (NL: 98-99)

The poles of a proposition (indicated by the letters ‘a’ and ‘b’)⁹ represent its possibility to be true or false. A proposition has two poles because it can be true and it can be false. And this amounts to its sense. As Wittgenstein will later say in the Notes Dictated to Moore:

‘[T]rue’ and ‘false’ are not accidental properties of a proposition, such that, when it has meaning, we can say it is also true or false: on the contrary, to have meaning means to be true or false: the being true or false actually constitutes the relation of the proposition to reality, which we mean by saying that it has meaning (Sinn [sense]) (NM: 113).

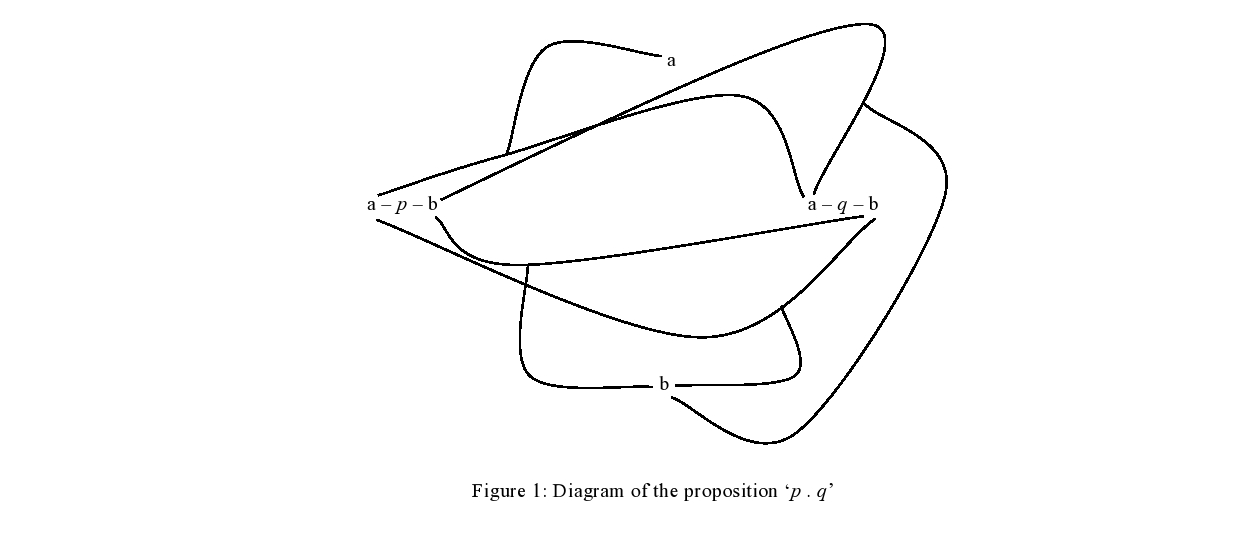
The proposition ‘p’ together with its poles for truth and falsehood is rendered by Wittgenstein as ‘a–p–b’. Poles are essential in the Notes on Logic’s account of molecular propositions, there called ab-functions (see NL: 102-103) and obtained by the application of ab-operations (see NL: 94). ‘not p’, for instance, is expressed in Wittgenstein’s notation as ‘b-a-p-b-a’; what the ab-operation ‘negation’ does is reversing the truth-poles of the proposition a-p-b, thus turning its a-pole into a b-pole and its b-pole into an a-pole, thereby getting as a result the formula ‘b-a-p-b-a’, with opposite sense. A different example, involving two elementary propositions, is the proposition ‘p and q’. In Wittgenstein’s ab-notation this proposition is expressed by means of a truth-diagram,¹⁰ similar to the one in figure 1.

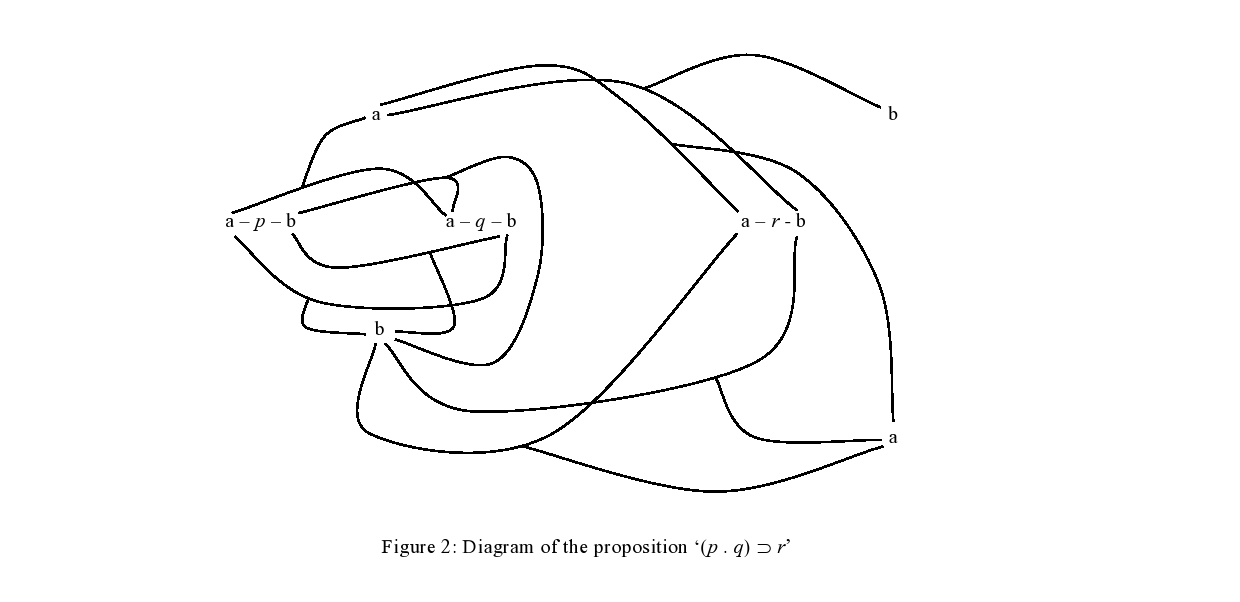
In the diagrammatical representation of a conjunctive proposition the outer a-pole (the true-pole) is only connected with the pairing of the a-poles of ‘p’ and ‘q’ (that is to say, with the possibility of ‘p’ and ‘q’ being both true), and the outer b-pole (the false-pole) is connected with all the other pairings of the poles of ‘p’ and ‘q’. Ab-functions, as well as elementary propositions, have ab-poles (are essentially true/false) and are thus bipolar in the same way in which elementary propositions are. This is made clear by truth-diagrams, which show how a molecular proposition gets its ab-poles (its sense) by correlation with the ab-poles of the original elementary proposition(s). Of course, Wittgenstein reminds us: “As the ab functions of atomic propositions are bi-polar propositions again we can perform ab operations on them. We shall, by doing so, correlate two new outside poles via the old outside poles to the poles of the atomic propositions” (NL: 94). That is: ab-operations can be iterated. This is again made visible by the truth-diagram method. The proposition ‘(p . q) ⊃ r’, for example, can be represented diagrammatically as shown in figure 2.

First the ab-poles of ‘p’ and ‘q’ are connected to determine the ab-poles of ‘p . q’ (as we saw in the previous diagram); then the ab-poles of ‘p . q’ are in turn connected to the ab-poles of ‘r’ to determine the ab-poles of the molecular proposition ‘(p . q) ⊃ r’.

We can see from the above examples that, on Wittgenstein’s account, the link between elementary and molecular propositions is provided by the notion of bipolarity, which in turn explains what it is for a proposition (elementary or not) to have sense. A proposition’s having ab-poles (truth-conditions, sense) is thus everything that is needed in order to account for logical relations between propositions, because ab-operations simply operate on elementary propositions’ ab-poles to generate new propositions with ab-poles, with truth-conditions. Despite the fact that there is no general statement, in the Notes on Logic, of the view that logical constants are implied in an elementary proposition, Wittgenstein’s account of the sense of a proposition in the Notes implements the general view that logical complexity is contained in (elementary) propositional interconnectedness. Elementary propositions already ensure the possibility of molecular propositions (and thus of logical com-plexity) because the latter simply consist in a rearrangement of the ab-poles of elementary propositions, ab-poles which are given by – and coincide with – a proposition’s having sense (bipolarity).¹¹

4. Language and logic in the Tractatus. Why an elementary proposition really contains all logical operations in itself

The account of the relation between elementary and molecular propositions sketched above is overall maintained in the Tractatus, Wittgenstein’s revision of his early account of propositional sense (and of the nature of propositional constituents) notwithstanding.¹² What there is in the Tractatus, which was not fully present in the Notes on Logic, is the conception of a proposition as a picture of reality,¹³ as having sense by depicting a particular situation (a state of affairs). “A proposition states something only in so far as it is a picture” (TLP 4.03). And: “Instead of, ‘This proposition has such and such a sense’, we can simply say, ‘This proposition represents such and such a situation’” (TLP 4.031). But having sense still means, for the Tractatus, to be true or false.

A proposition can be true or false only in virtue of being a picture of reality. (TLP 4.06)

And in the Notebooks he writes:

Only in this way can the proposition be true or false: It can only agree or disagree with reality by being a picture of a situation. (NB: 8)

In the Notebooks entry on 3.10.14 (repeated almost literally in the Tractatus at 4.032), Wittgenstein makes the relation between pictures and truth/falsity depend on the fact that pictures are essentially logically articulated. “The proposition is a picture of a situation only in so far as it is logically articulated”. Thus a “simple – non-articulated – sign can be neither true nor false” (NB: 8). A picture’s capability of being true or false thus depends on its having a structure, by means of which it represents (depicts) a state of affairs in reality. A picture is therefore a representational (or pictorial) structured fact, that is, a fact representing elements in reality to be combined as its elements are combined. By being a picture of reality a proposition is therefore intrinsically true or false: if things in reality are combined as it shows them to be then the proposition is true, and false otherwise. Wittgenstein’s Tractarian conception of a proposition also brings with it the view that a proposition depicts a situation, a state of affairs, and that the latter’s obtaining (or existing) makes the proposition true:

If an elementary proposition is true, the state of affairs exists: if an elementary proposition is false, the state of affairs does not exist. (TLP 4.25)¹⁴

Thus, possibilities of existence and non-existence of states of affairs determine the possibilities of truth and falsehood of their corresponding propositions: “Truth-possibilities of elementary propositions mean possibilities of existence and non-existence of states of affairs” (TLP 4.3). In the context of his discussion of truth-possibilities Wittgenstein introduces the familiar truth-tabular (T-F) notation; in the truth-tabular notation, a proposition ‘p’ is assigned T-F poles, that is, truth-possibilities, where “’T’ means ‘true’ [and] ‘F’ means false” (TLP 4.31). The bipolarity of propositions is thus reaffirmed: what Wittgenstein conceived of in terms of ab-poles in the Notes on Logic becomes, in the Tractatus, truth-possibilities, or truth-conditions.

Picturing (representing, saying), therefore, generates bipolarity: by picturing its subject “from a position outside it” (TLP 2.173), a picture represents it either correctly or incorrectly, and thus acquires truth-possibilities. As Thomas Ricketts observes:

The conception of elementary sentences as pictures makes their agreement or disagreement with reality – their possession of true-false poles, of sense – intrinsic to them. (Ricketts 1996: 80)

Truth-possibilities, T-F poles, are thus embedded into the very representational nature of a proposition, and are not determined by, for example, the judgemental or assertoric form with which a proposition can be expressed. As Wittgenstein had written in the Notes on Logic: “Judgment, question and command are all on the same level. What interests logic in them is only the unasserted proposition” (NL: 96). Judgement and assertion are, as Wittgenstein has it, merely psychological (see NL: 95), i.e. of no concern to logic. What is not psychological, because intimately related to truth and thus to logic, is a proposition’s sense, namely its representational structure, which gives it its T-F poles and thus makes it essentially true or false. (See the discussion in Johnston 2011.)

Truth-operations, as well as ab-operations, operate on propositions’ T-F poles to deliver propositions with T-F poles (bipolar propositions). It is important to stress that what an operation operates on is a proposition’s T-F poles (their truth-possibilities, or ab-poles according to Wittgenstein’s position in the Notes on Logic); the bases of the operation, say, ‘conjunction’ are strictly speaking ‘(TF)(p)’ and ‘(TF)(q)’, (‘a-p-b’, ‘a-q-b’ in the Notes on Logic) and not ‘p’ and ‘q’. The result of the operation – which in the truth-tabular notation takes the form ‘(FTTT)(p, q)’¹⁵ – makes it evident that ‘(TF)(p)’ and ‘(TF)(q)’ do not occur in it; this is another way of putting the thought from the Notes Dictated to G. E. Moore, discussed in section 3, that “one proposition can’t ‘occur’ in another” (see Sullivan 2000: 181).

It might be misleading to say, as I did in the previous paragraph, that operations operate on propositions’ T-F poles and deliver propositions with T-F poles, if this is taken literally. Once elementary propositions are given, in fact, by means of truth-operations all propositions can be obtained; this procedure can of course also produce propositions which are not bipolar, in that they do not have either a T-pole (contradictions) or a F-pole (tautologies). These propositions, the propositions of logic, are peculiar truth-functions because, unlike other truth-functions, are either true for all truth-possibilities of elementary propositions (tautologies) or false for all truth-possibilities of them (contradictions). In this sense, although they are the “extreme cases” (TLP 4.46) – or the “limiting cases” (TLP 4.466) – of the process of the truth-functional construction of propositions, they are integral part of that very process, integral “part of the symbolism” (TLP 4.4611). It is in this context, I believe, that Wittgenstein’s claim that “[i]f we know the logical syntax of any sign-language, then we have already been given all the propositions of logic” (TLP 6.124) should be read. When we know the logical syntax of language, thus when we know how signs signify and thus how they can be combined in meaningful symbols – propositions that are true or false – we already have all the propositions of logic, that is, we have the resources to operate on propositions’ truth-values to generate propositions which are true or false no matter what.

On Wittgenstein’s conception, thus, operations are rules for the construction of molecular propositions: they are not representatives, names of entities (cf. TLP 4.0312), such as Fregean functions or Russellian propositional functions; the proposition ‘p . q’, whose formulation in Russellian notation might encourage the idea that there is something corresponding to the dot, can – as seen above – be rewritten as ‘(FTTT) (p, q)’, where nothing corresponds to the logical constant. Again, Wittgenstein’s notation makes it clear that the molecular proposition in question does not contain anything over and above what is contained in the elementary propositions of which it is a truth-function, because there is no new material element, in it, which was otherwise missing from the elementary propositions ‘p’ and ‘q’.

This, however, might seem problematic on the lights of Wittgenstein’s claim that an elementary proposition really contains all logical operations – constants – in itself. Since an elementary proposition is an immediate concatenation of names, if logical operations were present in an elementary proposition, they would have to be names, and thus they would be representatives of objects, contrary to what Wittgenstein says at 4.0312. Clearly, therefore, Wittgenstein does not mean that, literally, logical operations are present in an elementary proposition, that is, contained in its sense.¹⁶ Our discussion of the notion of an operation, however, gives us the resources to understand what Wittgenstein means. Elementary propositions, by depicting reality truly or falsely, are correct or incorrect, and thus have truth-possibilities. This, as seen, is all that is needed to produce, by means of the application of operations, molecular propositions. Thus what elementary propositions really contain is the possibility of all logical operations, the possibility of generating all molecular propositions; in this sense they contain all logical operations in themselves. In the Notebooks entry on 5.11.14, quoted towards the end of section 1, Wittgenstein explicitly discusses the relation between an elementary proposition and its truth-functions by saying that the possibility of the latter is given as soon as the former is given.¹⁷ Elementary propositions’ T-F articulation (given by their being pictures of reality) makes them suitable for being logically operated on, and thus for potentially generating all truth-functional molecular propositions.¹⁸

5. Conclusion

We are now in a position to see fully why the bipartite reading, discussed in section 1, is wrong. According to it, there is no intrinsic connection between elementary propositions and the truth-functions obtained by the application of truth-operations on them, because to be an elementary proposition and to be a truth-function are quite different things. But Wittgenstein repeatedly remarks that nothing more than the sense of elementary propositions is needed in order to account for truth-functional articulation, and hence for logical complexity as a whole. Once the pictorial (and bipolar) character of a proposition is understood, then everything is given in order to understand how propositions can enter into logical relations with one another. Those relations are already implied by propositions’ own nature (their T-F articulation), by propositions’ determining their sense, hence by the conditions on which they are true or false. As Wittgenstein summarises this in the Notebooks: “The logical constants of the proposition are the conditions of its truth” (NB: 36). This is, ultimately, the reason why Wittgenstein claims, as seen at the end of section 2, that logical operations are already in place once a language has been established; their possibility is implied once we have a notation in which we express thoughts that are true or false.

And this, in turn, perfectly coheres with Wittgenstein’s view that, at bottom, there is only one logical constant, which is “what all propositions, by their very nature, had in common with one another”; this – Wittgenstein says – “is the general propositional form” (TLP 5.47), the “essence of the proposition” (TLP 5.471). The general form of the proposition is “a description of the propositions of any sign-language whatsoever” such that “every possible sense can be expressed by a symbol satisfying the description. […] The general form of a proposition is: This is how things stand” (TLP 4.5).¹⁹ The general propositional form is thus a proposition’s capability of expressing sense – representing reality – and thus being true or false. As Marie McGinn writes:

The general form of a proposition expresses […] what all propositions that represent states of affairs have in common. It is given as soon as a language in which we express judgements about the world is given. In acquiring language we have already grasped the general form of a proposition, that is, we have already grasped the whole of logic, the essence of representation as such. (2006: 240)

The bipartite reading however, presents a picture of the Tractarian conception of language that can hardly be reconciled with the idea that there is a general propositional form, an essence of representation, because on that view the essence of some propositions (elementary ones) is to be pictures, the essence of others (molecular ones) is to be truth-functions. But on Wittgenstein’s view every proposition is the value of the general propositional form, because propositions have a common essence (pictorial structure), by which they say that “such and such is the case”, and which makes them true or false.

We have seen, therefore, that on Wittgenstein’s view logical operations (the rules for the formation of molecular propositions) are given by – and implied in – the representational character of (elementary) propositions; their possibility is already given when we have elementary propositions depicting reality truly or falsely. This is the reason why logic as a whole, for Wittgenstein, is given at the level of elementary propositions, that is to say, is given as soon as propositions saying something about reality are given; a proposition’s having sense (depicting reality) is thus all that is needed to carry out logical operations, and thus to obtain molecular (and logical) propositions out of elementary ones; this is the core motivation for Wittgenstein’s idea that logical complexity is contained in – forms part of – linguistic complexity, and thus for his idea that an elementary proposition already contains all logical constants (operations) in itself. Thus, “[l]ogic is given as soon as a language in which we express judgements about the world is given; it is […] already complete or entire when we have a language that we use to say how things are” (McGinn 2006: 69).

If the one developed above is a correct reading of Wittgenstein’s view of logical complexity, we have thus reached an explanation of Wittgenstein’s conception of the unity of language and logic, of why the problems related to individual logical constants (the problem of logical complexity), as Wittgenstein repeatedly states, are only reflections of the “one great problem” (NB: 40), the problem of giving the essence of a proposition (TLP 5.471), and thus the essence (of the representational character) of language.²⁰

Biographical note

Daniele Mezzadri studied philosophy at the universities of Bologna, St. Andrews and Stirling, where he obtained his Ph.D. in 2010. His doctoral thesis addresses the relations between Wittgenstein’s philosophy of language and logic in the Tractatus and Frege’s and Russell’s conceptions of logic and judgment. His research interests are primarily in the early Wittgenstein and more broadly in the history of analytic philosophy and the philosophy of language and logic. He is currently Assistant Professor in the Department of Philosophy at UAE University in the U.A.E.